1.简介

二分查找

  • 最多查找 $\log_{2}n$ 次

  • 时间复杂度：$O(\log n)$

  • 有序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def binary_search(list, item):
    low = 0
    high = len(list) - 1 
while low <= high: 
    mid =(low + high)
    guess = list[mid]
    if guess == item:
        return mid
    # mid 如果不是，就从 mid 前后继续查找
    if quess > item: 
        high = mid - 1
    else:
        low = mid + 1
return None

旅行商问题

有一位旅行者需要前往 n 个城市，同时确保旅程最短（计算每种顺序及其总旅程）

$ O(n!) $


2.选择排序

需要将数据存储到内存时，我需要请求将数据提供存储地址，计算机会给我一个存储地址，我再把数据放里面

数组

  • 需要连续的存储空间，如果不满足，无法添加数据，则复制（移动）到另一个满足的连续空间

  • 解决方法：预留空间，会浪费内存

  • 支持随机访问和顺序访问

链表

  • 每个元素都存储下一个元素的地址

  • 修改和删除简单，只需修改一两个元素指向的地址

  • 缺点：最后一个元素不能直接读取

  • 只能顺序访问（从第一个元素开始逐个读取元素）

选择排序

  • 选择单一指标进行排序

  • 每次遍历一遍 选一个出来

  • 时间复杂度：$ O（n^2） $

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def findSmallest(arr: List[int]) ->int:
    '''
    定义一个找出数组中最小数的函数，返回其索引
    '''
    smallest = arr[0]
    smallest_index = 0
    
    for i in range(1, len(arr)):
        if arr[i] < smallest:
            smallest = arr[i]
            smallest_index = i
    return smallest_index
    
def selectionSort(arr)
    '''
    选择排序
    '''
    newarr = []
    for i in range(1, len(arr)):
        smallest_index = findSmallest(arr)
        smallest = arr.pop(smallest_index)
        # 使用内置函数实现
        # smallest = min(arr)
        # app.remove(smallest)
        newarr.append(smallest)
    return newarr

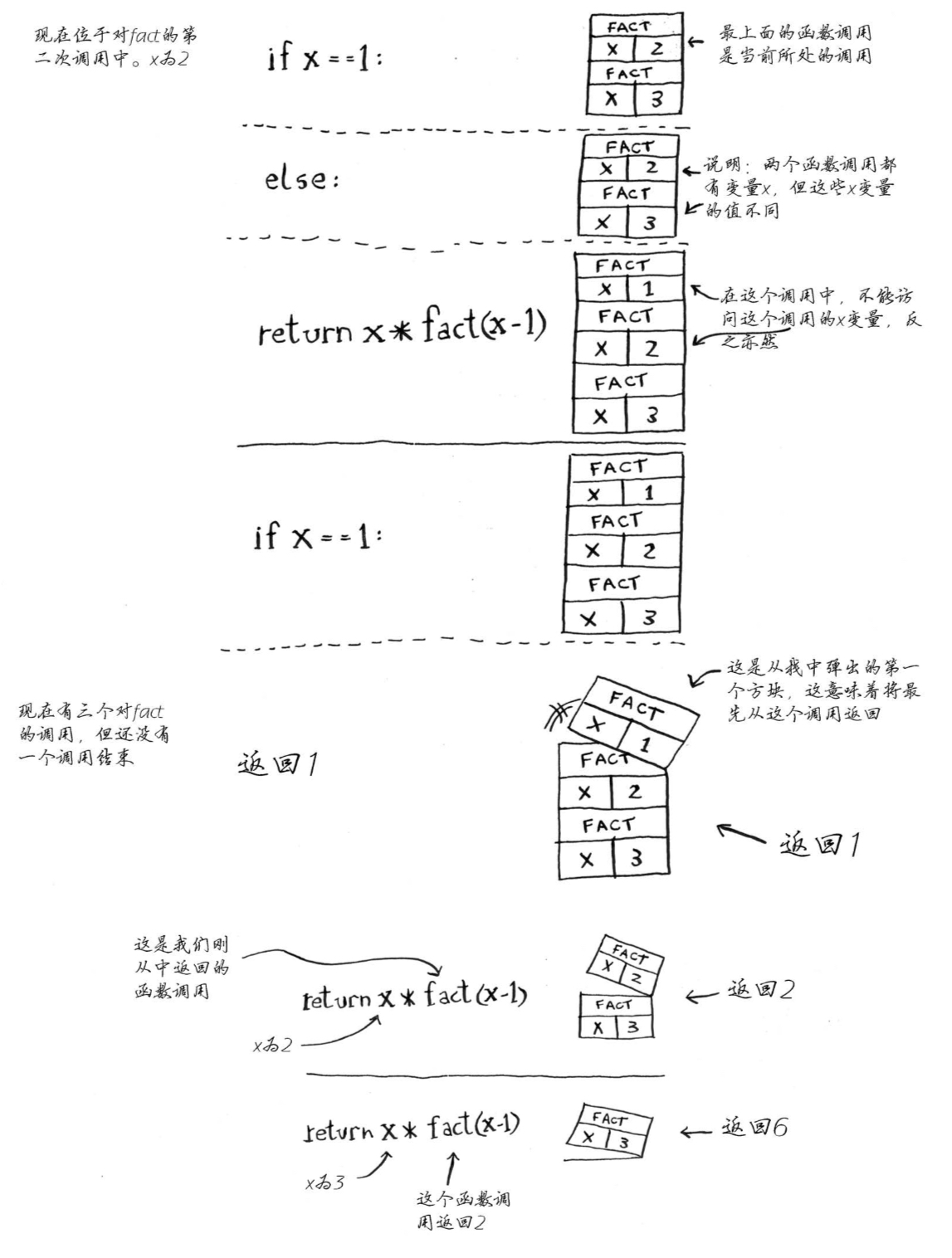
3.递归

请手写递归逻辑

编写递归函数，必须注意何时停止递归

  • 递归条件：函数调用自己

  • 基线条件：函数不再调用自己

栈

  • 操作

    • 压入

    • 弹出

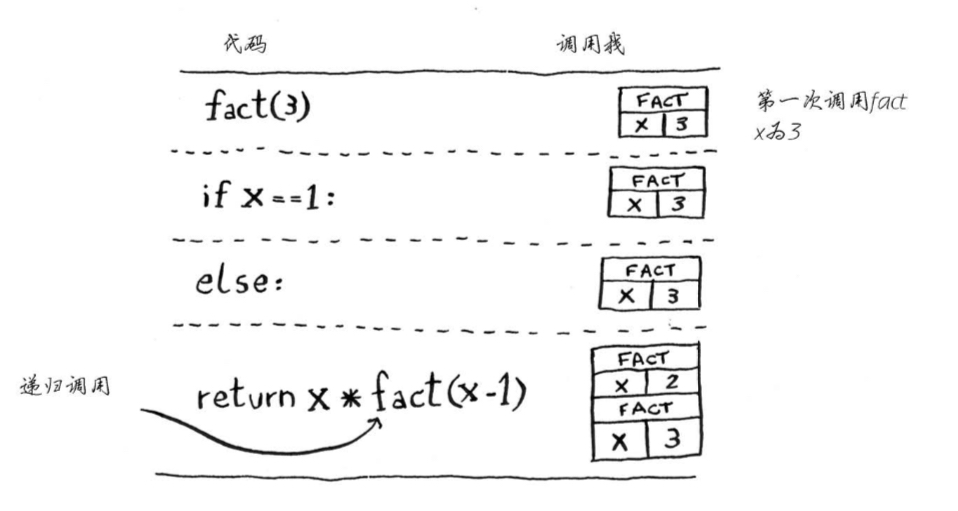
  • 调用栈(call stack)

  • 函数与栈

    • 函数就是栈

    • 哪个函数在栈顶就执行哪个函数

    • 调用另一个函数时，当前函数暂停并处于未完成状态

    • 调用函数——压栈

    • return——出栈

快速排序

分而治之（divide and conquer, D&C）

  • 步骤
    • 找出基线条件
    • 不断将问题分解（缩小规模），直到符合基线条件

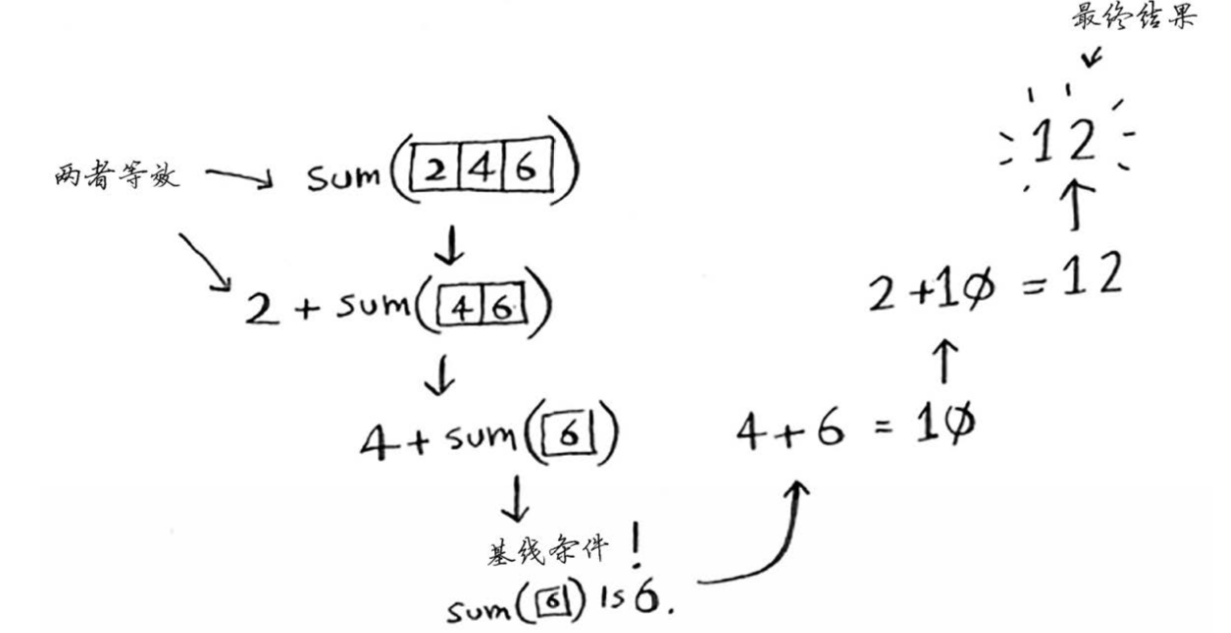
  • 例子：sum函数

    Untitled

    1
    2
    3
    4
    5
    6
    def sum_arr(arr):
        if not arr:
            return 0
        else:
            number = arr.pop()
            return number + sum_arr(arr)

  • 提示：涉及数组的递归函数，基线条件一般是数组为空或只有一个元素

  • 提示：python数组是可变的，传进函数的是数组本身

快速排序

  • 基线条件：数组为空或只包含一个元素
  • 复杂度：O(nlogn)
  • 首先选择一个元素——基准值
  • 接着分区
    • 一个小于基准值的子数组
    • 基准值
    • 一个大于基准值的子数组
  • 对这两个子数组基进行快速排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def quicksort(array):
    if len(array) < 2:
        # 基线条件
        return array
    else:
        # 取基准值
        pivot = array[0]
        # 一个小于基准值的子数组
        less = [i for i in array[1:] if i<=pivot]
        # 一个大于基准值的子数组
        greater = [i for i in array[1:] if i>pivot]
        
        return quicksort(array) + pivot + quicksort(array)
        
    print quicksort([arr])

4.散列表

散列函数

复杂度：$ O(1)$

条件：

  • 必须是一致的，输入和输出一一对应
  • 将不同的输入映射到不同的数字
  • 灵活运用索引
  • 只返回有效索引

python：字典 

1
2
3
4
5
6
7
8
9
book = dict()
book["apple"] = 0.67
book["milk"] = 1.49
book["avocado"] = 1.49
print(book)
print(f"book")
print(book.items())
print(book.keys())
print(book.values())

散列表由键和值组成

散列表的应用

  • 电话簿
  • 网站地址转IP地址
  • 缓存
1
2
3
4
5
6
7
8
cache ={}
def get_page(url):
    if cache.get(url):
        return cache[url]
    else:
        data = get_data_from_server(url)
        cache[url] = data
        return data
  • 防止重复
1
2
3
4
5
6
7
8
# 创建已投票字典
voted = {}
def check_voter(name): 
    if voted.get(name):
        print "kick them out!" 
    else:
        voted[name] = True
        print "let them vote!"

冲突

给两个键分配的位置相同

  • 散列函数很重要
  • 如果散列表存储的链表很长，散列表的速度将急剧下降

性能

  • 较低的填装因子
  • 良好的散列函数

填装因子：散列表包含的元素数/位置总数

一旦填装因子大于0.7，可以调整列表长度

5.广度优先搜索

breadth-first search, BFS

效果：找到两样东西之间的最短距离

最短路径问题(shortest-path problem)

  • 我去北京天安门，需要几个步骤
    • 打车到广州南站
    • 高铁从广州南站到北京
    • 打车到北京天安门
  • 使用图来建立问题模型
  • 使用广度优先搜索解决问题

图

图模拟一组连接

图由节点(node)和边(edge)组成

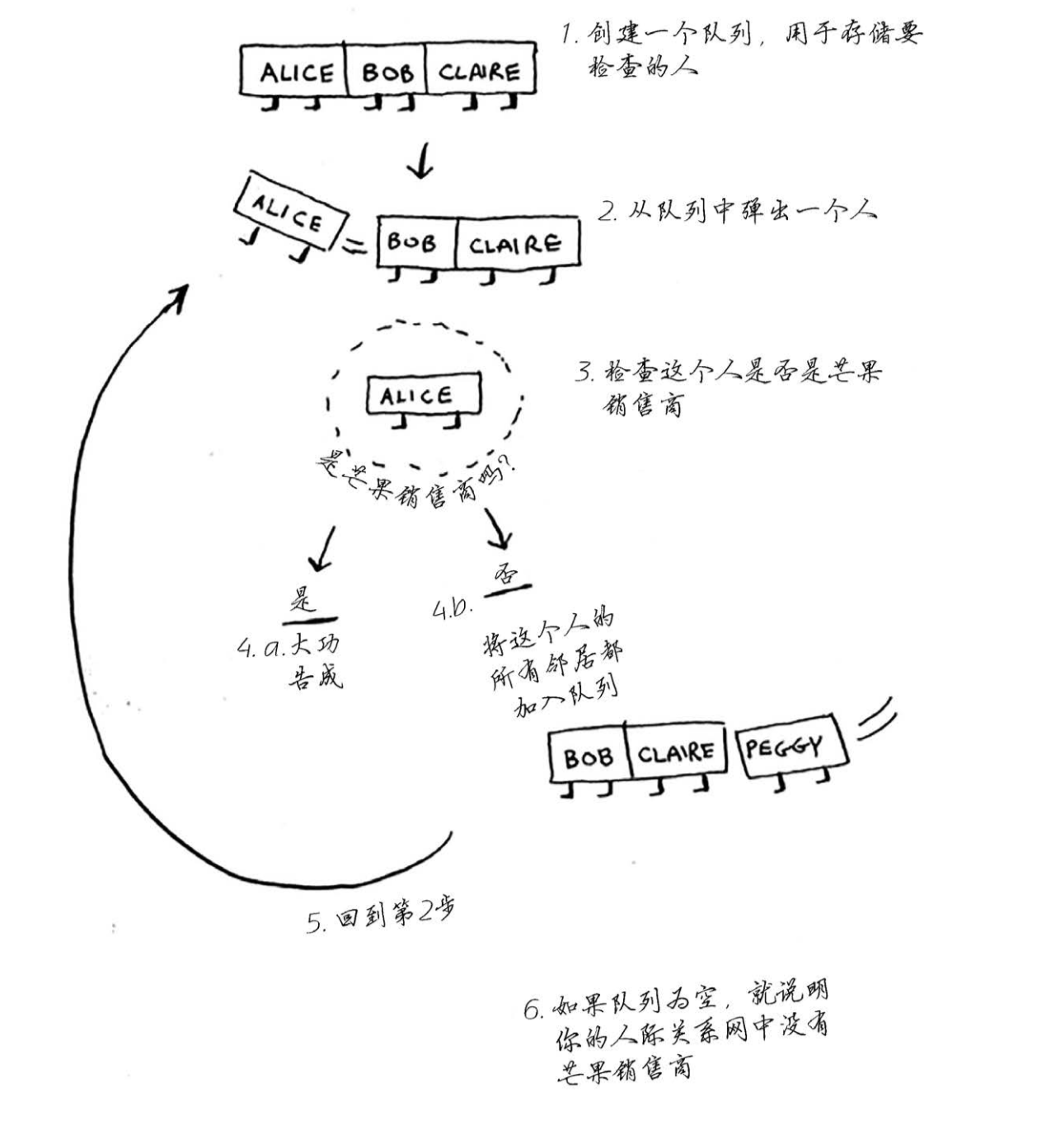
广度优先搜索

解决问题：

  1. 从节点A出发，有前往节点B的路径吗？
  2. 从节点A出发，前往节点B的哪条路经最短？

队列

先进先出(First In First Out, FIFO)

操作：

  • 入队
  • 出队
1
2
3
4
5
6
7
8
9
graph = {}
graph["you"] = ["alice", "bob", "claire"]
graph["bob"] = ["anuj", "peggy"]
graph["alice"] = ["peggy"]
graph["claire"] = ["thom", "jonny"]
graph["anuj"] = []
graph["peggy"] = []
graph["thom"] = []
graph["jonny"] = []

键-值对的添加顺序不重要，散列表是无序的

🔥实现算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from collections import deque

def person_is_seller(name):
    return name[-1] == 'm'

def search(name):
    search_queue = deque()
    search_queue += graph["you"]
    searched = [] # 记录检查过的人

    while search_queue:# 只要队列不为空
        # 取出队列的第一个人
        person = search_queue.popleft()
        if person not in searched:
            if person_is_seller(person):
                print(person + "is a mango seller!")
                return True
            else:	
                # 将其邻居加入队列
                search_queue += graph[person]
        return False
        
search("you")

运行时间

O(V + E) V是顶点数，E为边数

拓扑排序是针对有向无环图（DAG，Directed Acyclic Graph）的一种排序算法，它将图中的所有顶点排成一个线性序列（有序序列），使得对于任何一条有向边U→V，顶点U都在顶点V之前

树是特殊的图，其中没有往后指的边

6.迪克斯特拉算法

广度优先搜索 找出段数最少的路径

迪克斯特拉算法 找出最快、总权重最小的路径

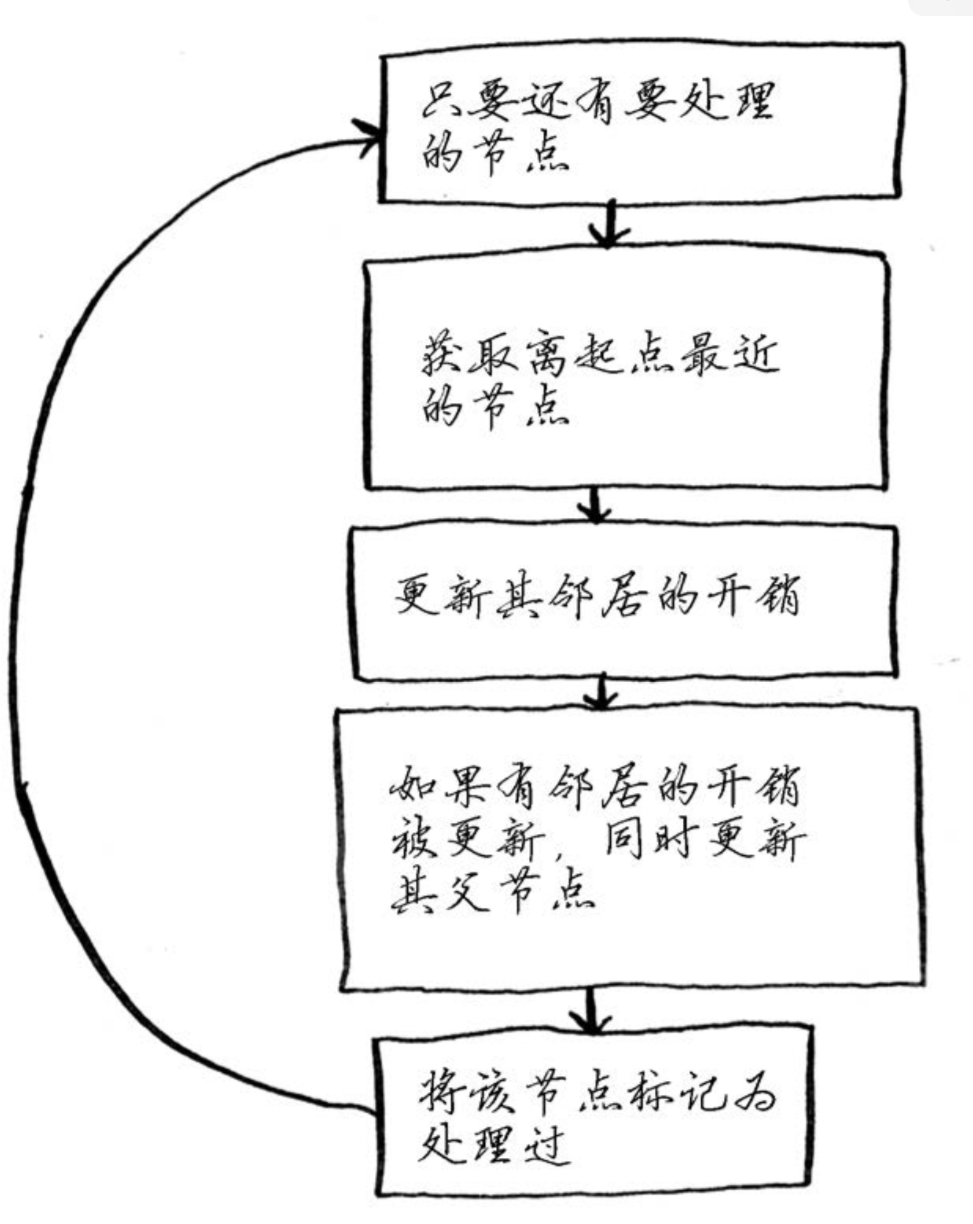
  1. 找出最小的节点（本轮权重最小的节点）
  2. 更新该节点的邻居的开销
  3. 重复🔁该过程，直到遍历完所有节点
  4. 计算最终路径

🍁 找出图中最便宜的节点，并确保没有到该节点的更便宜的路径

术语

  • 权重(weight)
  • 加权图(weighted graph)
  • 非加权图(unweighted graph)
  • 环(loop)

迪克斯特拉算法只适用于有向无环图(directed acyclic graph, DAG)

负权边

如果有负权边，就不能使用迪克斯特拉算法

可以使用贝尔曼-福德算法(Bellman-Ford algorithm)

实现

需要三个散列表

  1. 一个散列表存储邻居和前往邻居的开销（邻居的散列表包含开销的散列表）
  2. 一个散列表存储每个节点的开销（从起点开始计算🧮），终点默认为无穷大
  3. 一个散列表存储父节点，默认为没有None
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 更新最小的节点
node = find_lowest_cost_node(costs) 
while node is not None:
    # 获取该节点的开销和邻居散列表
    cost = costs[node] 
    neighbors = graph[node] 
    for node in neighbors.keys():
    # 遍历当前节点的所有邻居
        new_cost = cost + neighbors[n] 
        if costs[node] > new_cost:
        # 如果经当前节点前往该邻居更近，就更新该邻居的开销
            costs[node] = new_cost
            # 同时将该邻居的父节点设置为当前节点
            parents[node] = node   
    processed.append(node)
    node = find_lowest_cost_node(costs)
    
def find_lowest_cost_node(costs):
    '''
    从costs散列表找出开销最小的节点
    '''
    lowest_cost = float("inf")
    lowest_cost_node = None
    for node in costs:
        cost =costs[node]
        if cost < lowest_cost and node not in processed:
        # 如果当前节点的开销更小且未处理过
            lowest_cost = cost
            lowest_cost_node = node
    return lowest_cost_node

练习

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
graph = {}
graph["start"] = {}
graph["a"] = {}
graph["b"] = {}
graph["c"] = {}
graph["d"] = {}
graph["start"]["a"] = 5
graph["start"]["b"] = 2
graph["a"]["c"] = 4
graph["a"]["d"] = 2
graph["b"]["a"] = 8
graph["b"]["d"] = 7
graph["c"]["d"] = 6
graph["c"]["fin"] = 3
graph["d"]["fin"] = 1
graph["fin"] = {}
costs = {}
inf = float("inf")
costs["a"] = 5
costs["b"] = 2
costs["c"] = inf
costs["d"] = inf
costs["fin"] = inf
parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = None
processed = []
    
def find_lowest_cost_node(costs):
    '''
    从costs散列表找出开销最小的节点
    '''
    lowest_cost = float("inf")
    lowest_cost_node = None
    for node in costs:
        cost =costs[node]
        if cost < lowest_cost and node not in processed:
        # 如果当前节点的开销更小且未处理过
            lowest_cost = cost
            lowest_cost_node = node
    return lowest_cost_node
    
# 更新最小的节点
node = find_lowest_cost_node(costs) 
while node is not None:
    # 获取该节点的开销和邻居散列表
    cost = costs[node] 
    neighbors = graph[node] 
    for neighbor_node in neighbors.keys():
    # 遍历当前节点的所有邻居
        new_cost = cost + neighbors[neighbor_node] 
        if costs[neighbor_node] > new_cost:
        # 如果经当前节点前往该邻居更近，就更新该邻居的开销
            costs[neighbor_node] = new_cost
            # 同时将该邻居的父节点设置为当前节点
            parents[neighbor_node] = node   
    processed.append(node)
    node = find_lowest_cost_node(costs)
    
print(costs["fin"])

🌍 所有东西都要初始化

7.贪婪算法

每步都选择局部最优解，最终得到的就是全局最优解

背包问题🎒

集合覆盖问题

  • 近似算法(approximation algorithm)
  • 选出一个覆盖了最多的未覆盖州的广播台
  • 重复直到覆盖掉所有州
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
provinces_needed = set(["京","津","冀","沪","黑","琼","粤"])
stations = {}
stations["北京"] = set(["京","津","冀"])
stations["天津"] = set(["津","冀","沪"])
stations["上海"] = set(["冀","沪","黑"])
stations["黑龙江"] = set(["冀","黑","琼"])
stations["海南"] = set(["琼","粤"])
stations["广东"] = set(["京","沪","粤"])
final_stations = set()

while provinces_needed:
    best_station = None
    states_covered = set()
    for station, states_for_station in stations.items():
        covered = provinces_needed & states_for_station
        if len(covered) > len(states_covered):
            best_station = station
            states_covered = covered
    final_stations.add(best_station)
    provinces_needed -= states_covered

print(final_stations)

创建集合，一个无序的不重复元素序列，set add remove ，交集&、并集｜、差集-

NP完全问题

需要计算所有的解，并从中选出最小/最短的

阶乘函数(factorial function)

NP完全问题的特征

  • 涉及所有组合的
  • 必须考虑各种可能的情况
  • 涉及序列且难以解决
  • 涉及集合且难以解决
  • 可转换为旅行商问题

8.动态规划

背包问题

简单算法：尝试各种组合，找出价值最高的组合($2^n$)

动态规划

  • 先解决子问题，再逐步解决大问题
  • 都从网格开始
    • 各行 为可选择的商品
    • 各列 为不同容量的背包

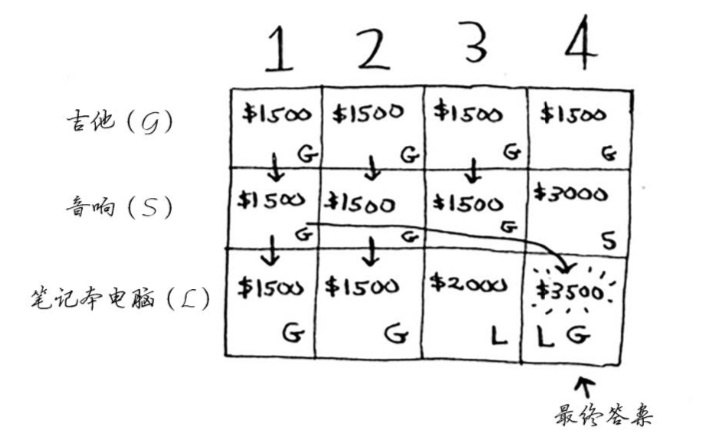
吉他行

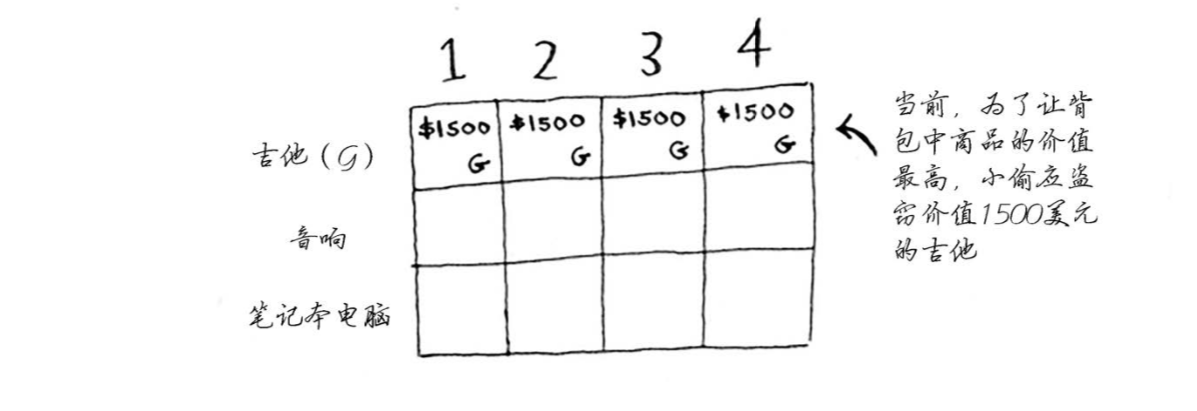
为了让当前的最大价值最大，在只能偷吉他的情况下，在1、2、3、4磅的背包容量单元格只能填¥1500

音响行

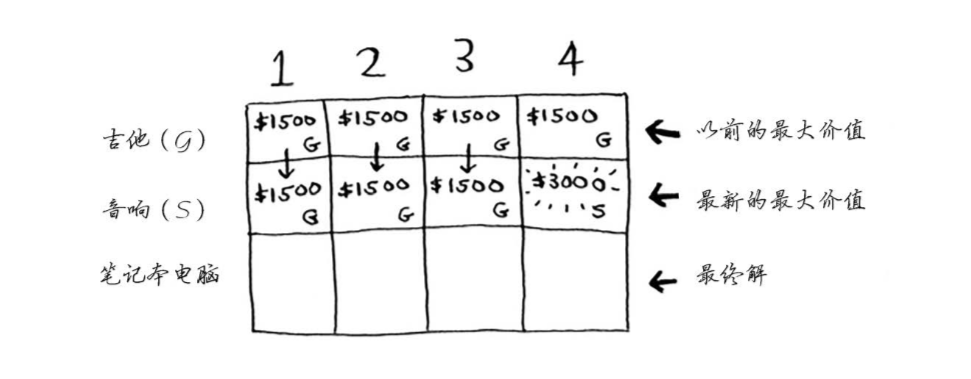
为了让当前的最大价值最大，在只能偷吉他和音响的情况下，在1、2、3磅的背包容量单元格只能填¥1500，因为音响太重了，在4磅的背包单元格终于可以填音响，更新为¥3000

笔记本行

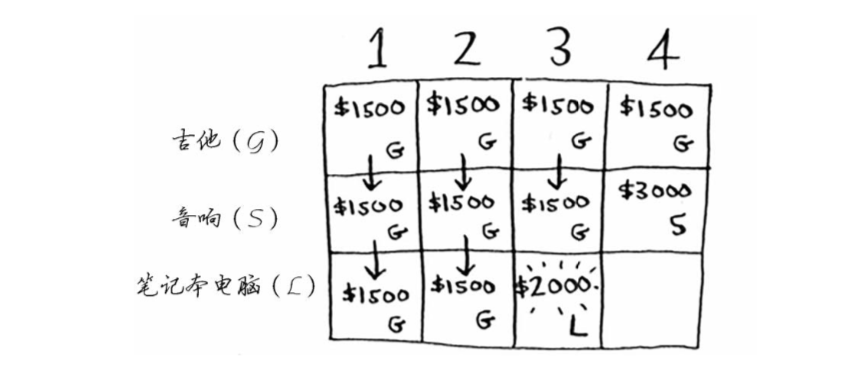
笔记本较重，3磅的背包容量单元格可以装下笔记本，更新为¥2000

Untitled

在4磅1的背包容量单元格可以同时装下吉他和笔记本，更新为¥3500

总结

Untitled

  • 沿着一列往下走时，最大价值不可能降低
  • 行的排列顺序与结果无关
  • 逐行or逐列排序都没有关系
  • 增加一件更小的商品会增加颗粒度，必须调整网络
  • 不可以偷商品的一部分
  • 旅游行程最优化可以使用背包问题

但仅当每个子问题都是离散的，即不依赖于其他子问题时，动态规划才管用

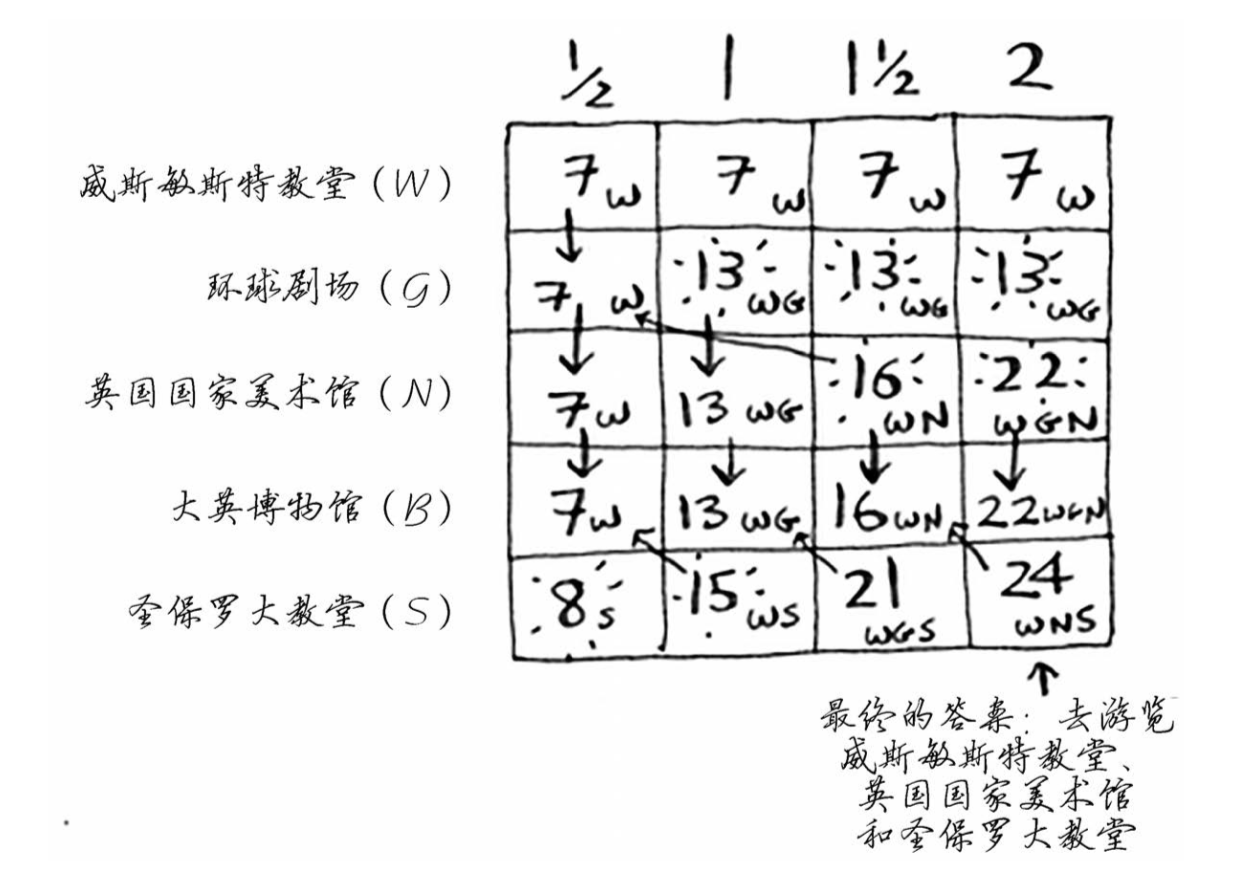
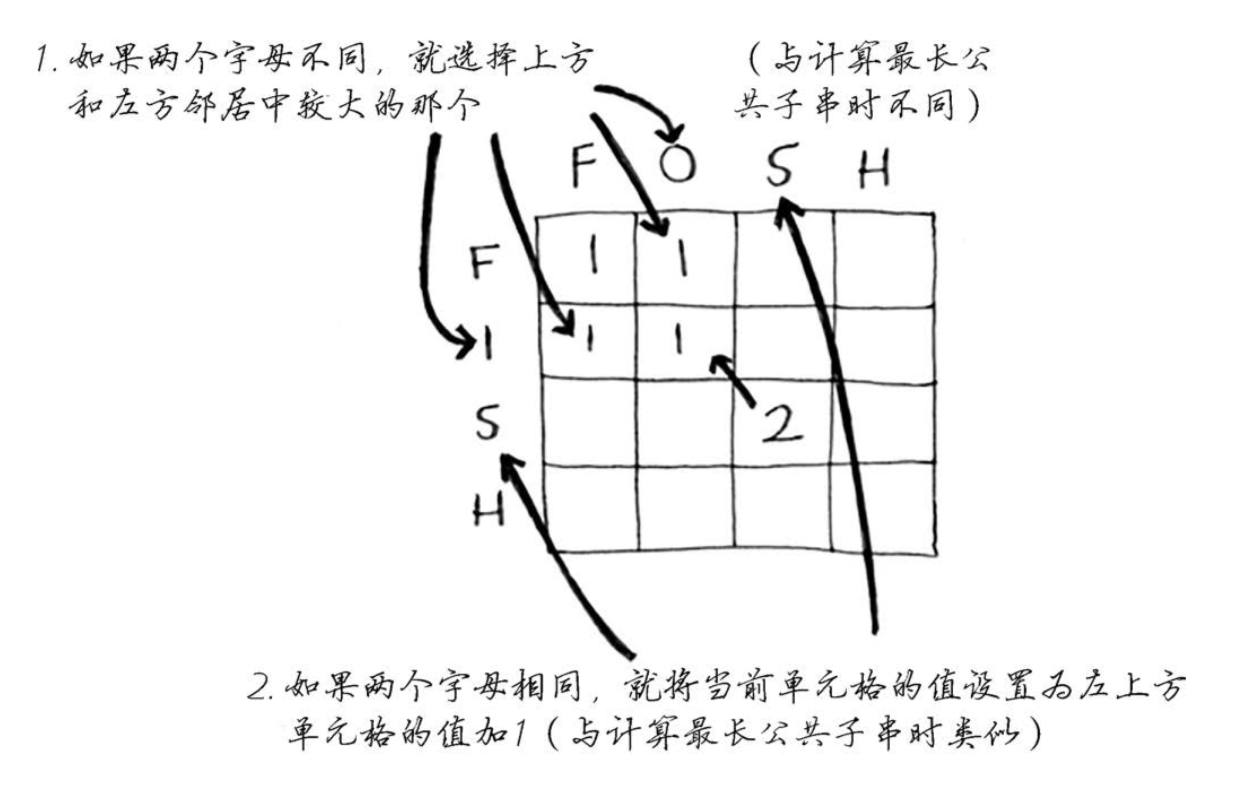
最长公共子串

1
2
3
4
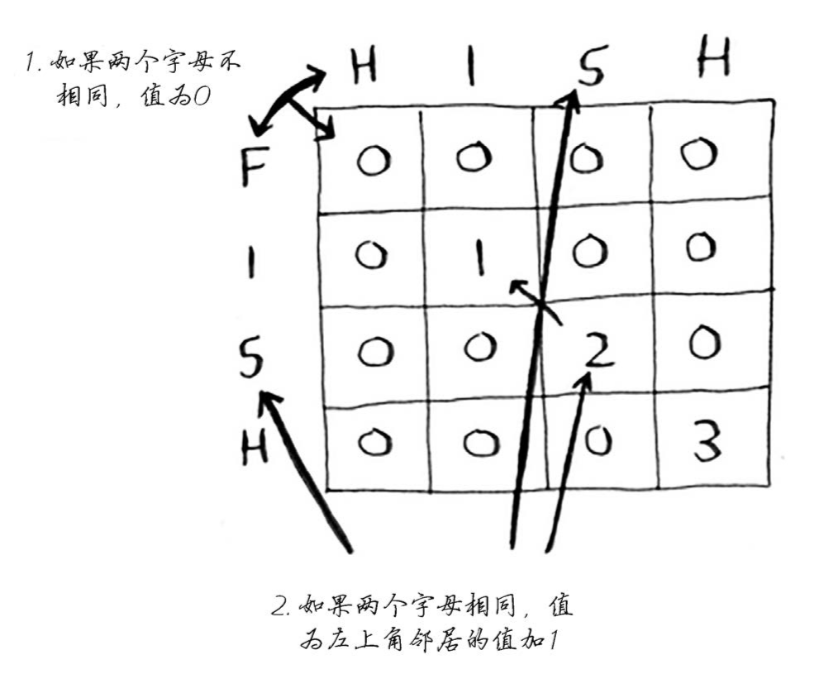
if word_a[i] == word_b[j]: # 如果相同设为左上角+1
    cell[i][j] = cell[i-1][j-1] + 1
else: # 如果不同设为0
    cell[i][j] = 0

答案为网格中最大的数字

最长公共子序列

Untitled

1
2
3
4
if word_a[i] == word_b[j]: # 如果相同设为左上角+1
    cell[i][j] = cell[i-1][j-1] + 1
else: # 如果不同设为0
    cell[i][j] = max(cell[i-1][j],cell[i][j-1])

9.K最近邻算法

k-nearest neighbors, KNN

  1. 对水果进行分类，比如哈密瓜🍈和西瓜🍉中有一个神秘的水果
  2. 查看它三个最近的邻居
  3. 在这些邻居中，哈密瓜🍈数量多于西瓜🍉，因此很可能是哈密瓜

创建推荐系统

特征抽取

计算两点的距离可以用毕达哥斯拉公式

余弦相似度

余弦相似度的取值范围从-1到1：

  • 1 表示向量完全相同（指向同一方向）
  • 0 表示向量正交（完全不同）
  • 1 表示向量完全相反（指向相反方向）

计算公式

对于两个向量 A 和 B，余弦相似度cosine(A,B) 定义为：

$\text{cosine}(\mathbf{A}, \mathbf{B}) = \frac{\mathbf{A} \cdot \mathbf{B}}{|\mathbf{A}| |\mathbf{B}|}$

其中：

  • A⋅B 是向量 A 和 B 的点积（内积）
  • ∥A∥ 和 ∥B∥ 分别是向量 A 和 B 的欧几里得范数（长度）

$\text{cosine}(\mathbf{A}, \mathbf{B}) = \frac{\sum{i=1}^{n} a_i \cdot b_i}{\sqrt{\sum{i=1}^{n} ai^2} \cdot \sqrt{\sum{i=1}^{n} b_i^2}}$

实例

假设有两个向量A=[a1,a2,a3]和B=[b1,b2,b3]，它们的余弦相似度计算如下：

$\text{cosine}(\mathbf{A}, \mathbf{B}) = \frac{a_1 b_1 + a_2 b_2 + a_3 b_3}{\sqrt{a_1^2 + a_2^2 + a_3^2} \cdot \sqrt{b_1^2 + b_2^2 + b_3^2}}$。

若是评价标准不同呢？

可使用归一化(normalization)。你可计算每位用户的平均评分，并据此来调整用户的评分

回归

就是根据已有数据预测结果（如一个数字）

🏆 KNN — 分类和回归

建议根据sqrt(n)来推荐

机器学习简介

OCR(optical character recognition)，光学字符识别

  1. 浏览大量的数字图像，提取特征（线段、点、曲线等）
  2. 遇到新图像时，提取该特征并找出最近的邻居都是谁

创建垃圾邮件过滤器

朴素贝叶斯分类器(Naive Bayes classifier)

假设特征之间相互独立

$P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}$

$y = \arg\max{C_i} P(C_i|X) = \arg\max{C_i} \frac{P(X|C_i) \cdot P(C_i)}{P(X)}$

预测股票情绪

几乎不可能

10.总结

  • 第一章
    • 二分查找的速度比简单查找快得多
    • O(log n)比O(n)快。需要搜索的元素越多，前者比后者就快得越多
    • 算法运行时间并不以秒为单位
    • 算法运行时间是从其增速的角度度量的
    • 算法运行时间用大O表示法表示
  • 第二章
    • 计算机内存犹如一大堆抽屉
    • 需要存储多个元素时，可使用数组或链表
    • 数组的元素都在一起
    • 链表的元素是分开的，其中每个元素都存储了下一个元素的地址
    • 数组的读取速度很快
    • 链表的插入和删除速度很快
    • 在同一个数组中，所有元素的类型都必须相同(都为int、double等)
  • 第三章
    • 递归指的是调用自己的函数
    • 每个递归函数都有两个条件:基线条件和递归条件
    • 栈有两种操作:压入和弹出
    • 所有函数调用都进入调用栈
    • 调用栈可能很长，这将占用大量的内存
    • 每次递归会创建新的栈帧，循环始终使用一个栈帧
  • 第四章
    • D&C将问题逐步分解。使用D&C处理列表时，基线条件很可能是空数组或只包含一个元素的数组
    • 实现快速排序时，请随机地选择用作基准值的元素。快速排序的平均运行时间为O（n logn）
    • 大O表示法中的常量有时候事关重大，这就是快速排序比合并排序快的原因所在
    • 比较简单查找和二分查找时，常量几乎无关紧要，因为列表很长时，O（log n）的速度比O（n）快得多
  • 第五章
    • 你可以结合散列函数和数组来创建散列表
    • 冲突很糟糕，你应使用可以最大限度减少冲突的散列函数
    • 散列表的查找、插入和删除速度都非常快
    • 散列表适合用于模拟映射关系
    • 一旦填装因子超过0.7，就该调整散列表的长度
    • 散列表可用于缓存数据（例如，在Web服务器上）
    • 散列表非常适合用于防止重复
  • 第六章
    • 广度优先搜索指出是否有从A到B的路径
    • 如果有，广度优先搜索将找出最短路径
    • 面临类似于寻找最短路径的问题时，可尝试使用图来建立模型，再使用广度优先搜索来解决问题
    • 有向图中的边为箭头，箭头的方向指定了关系的方向，例如，rama radit表示rama欠adit钱
    • 无向图中的边不带箭头，其中的关系是双向的，例如，ross - rachel表示 “ross 与rachel约会，而rachel也与ross约会”
    • 队列是先进先出（FIFO）的。
    • 栈是后进先出（LIFO）的。
    • 你需要按加入顺序检查搜索列表中的人，否则找到的就不是最短路径，因此搜索列表必须是队列
    • 对于检查过的人，务必不要再去检查，否则可能导致无限循环
  • 第七章
    • 广度优先搜索用于在非加权图中查找最短路径
    • 迪克斯特拉算法用于在加权图中查找最短路径
    • 仅当权重为正时狄克斯特拉算法才管用
    • 如果图中包含负权边，请使用贝尔曼-福德算法
  • 第八章
    • 贪婪算法寻找局部最优解，企图以这种方式获得全局最优解
    • 对于NP完全问题，还没有找到快速解决方案
    • 面临NP完全问题时，最佳的做法是使用近似算法
    • 贪婪算法易于实现、运行速度快，是不错的近似算法
  • 第九章
    • 需要在给定约束条件下优化某种指标时，动态规划很有用
    • 问题可分解为离散子问题时，可使用动态规划来解决
    • 每种动态规划解决方案都涉及网格
    • 单元格中的值通常就是你要优化的值
    • 每个单元格都是一个子问题，因此你需要考虑将问题分解为子问题
    • 没有放之四海皆准的计算动态规划解决方案的公式
  • 第十章
    • KNN用于分类和回归，需要考虑最近的邻居
    • 分类就是编组
    • 回归就是预测结果(如数字)
    • 特征抽取意味着将物品(如水果或用户)转换为一系列可比较的数字
    • 能否挑选合适的特征事关KNN算法的成败